SIR Model - The Flue Season - Dynamic Programming

# The SIR Model (susceptible, infected, and recovered) model is a common and useful tool in epidemiological modelling.

# In this post and in future posts I hope to explore how this basic model can be enriched by including different population groups or disease vectors.

# Simulation Population Parameters:
  # Proportion Susceptible
  Sp = .9

  # Proportion Infected
  Ip = .1

  # Population
  N = 1000

  # Number of periods
  r = 200

  # Number of pieces in each time period.
  # A dynamic model can be simulated by dividing each dynamic period into a sufficient number of discrete pieces.
  # As the number of pieces approaches infinity then the differences between the simulated outcome and the outcome achieved by solving the dynamic equations approaches zero.
  np = 1

# Model - Dynamic Change
  DS = function() -B*C*S*I/N
  DI = function() (B*C*S*I/N) - v*I
  DZ = function() v*I
  # I is the number of people infected, N the number of people in total, S is the number of people susceptible for infection, and Z is the number of people immune to the infection (from already recovering from the infection).

# Model Parameters:
  # Transmition rate from contact with an infected individual.
  B = .2
  # Contact rate.  The number of people that someone becomes in contact with sufficiently to recieve transmition.
  C = .5
  # Recovery rate. Meaning the average person will recover in 20 days (3 weeks).
  # This would have to be a particularly virolent form of the flu (not impossible at all).
  v = .05

# Initial populations:

  # Sesceptible population, Sv is a vector while S is the population values as the current period
  Sv = S = Sp*N

  # Infected, Iv is a vector while I is the population values as the current period
  Iv = I = Ip*N

  # Initial immunity.
  Zv = Z = 0

# Now let's how the model works.
  # Loop through periods
  for (p in 1:r) {
    # Loop through parts of periods
    for (pp in 1:np) {
   
      # Calculate the change values
      ds = DS()/np
      di = DI()/np
      dz = DZ()/np
 
      # Change the total populations
      S = S + ds
      I = I + di
      Z = Z + dz
   
      # Save the changes in vector form
      Sv = c(Sv, S)
      Iv = c(Iv, I)
      Zv = c(Zv, Z)
    }
  }

# ggplot2 generates easily high quality graphics
require(ggplot2)

# Save the data to a data frame for easy manipulation with ggplot
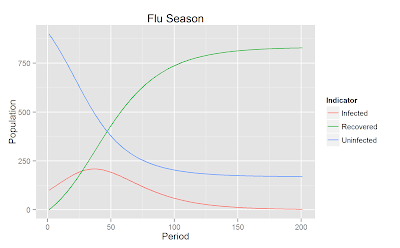
mydata = data.frame(Period=rep((1:length(Sv))/np,3), Population = c(Sv, Iv, Zv), Indicator=rep(c("Uninfected", "Infected", "Recovered"), each=length(Sv)))

# This sets up the plot but does not actually graph anything yet.

p = ggplot(mydata, aes(x=Period, y=Population, group=Indicator))  

 # This graphs the first plot just by the use of the p command.
 # Adding the geom_line plots the lines changing the color or the plot for each indicator (population group)
 p + geom_line(aes(colour = Indicator)) + ggtitle("Flu Season")

 # Save initial graph:
 ggsave(file="2013-05-14flu.png")

 # Let's do some back of the envelope cost calculations.
 # Let's say the cost of being infected with the flu is about $10 a day (a low estimate) in terms of lost productivity as well as expenses on treatment.
 # This amounts to:
 sum(Iv/np)*10
 # Which is a cost of $165,663.40 over an entire flu season for the thousand people in our simulated sample.
 # Or about $165 per person.

 # Imagine if we could now do a public service intervention.
 # Telling people to wash their hands, practice social distancing, and avoid touching their noses and eyes, and staying at home when ill.
 # Let's say people take up these practices and it reduces the number of potential exposure periods per contact by half.
 C = .25

 # ....

 p + geom_line(aes(colour = Indicator)) + ggtitle("Flu Season with Prevention")

  # Save initial graph:
 ggsave(file="2013-05-14flu2.png")

 # ....

  sum(Iv/np)*10
 # Which is a cost of $76,331.58 over an entire flu season  for the thousand people in our simulated sample or about 76 dollars per person.

 # The difference in costs is about 89 thousand dollars for the whole population or on average 89 per person.  The argument is therefore, so long as a public service intervention that reduces personal contact costs less than 89 thousand dollars for those 1000 people, then it is an efficient intervention (at least by the made up parameters I have here).